Maize
MAIZE Module Scope
The maize module simulates the growth of a maize crop in a daily time-step (on an area basis not single plant). Maize growth in this model responds to climate (temperature, rainfall and radiation from the input module), soil water supply (from the soilwat module) and soil nitrogen (from the soiln module). The maize module returns information on its soil water and nitrogen uptake to the soilwat and soiln modules on a daily basis for reset of these systems. Information on crop cover is also provided to the soilwat module for calculation of evaporation rates and runoff. Maize stover and root residues are ‘passed’ from maize to the residue and soiln module respectively at harvest of the maize crop. A list of the module outputs is provided in the ‘Maize module outputs’ section below, but basically the module will predict leaf area development, N% and biomass of stover; depth, N% and biomass of roots; grain N% and biomass; grain yield and N%, grain size and grain number all on a daily basis.
Maize Module History
The maize module was developed from a combination of the approaches used in the CM-KEN (Keating et al., 1991, 1992) and CM-SAT (Carberry et al., 1989; Carberry and Abrecht, 1991) models of maize (both derivatives of CERES-Maize, Jones and Kiniry, 1986), with some features of the maize model of Wilson et al. (1995). The major differences from CERES-Maize are routines which kill crops in response to severe water deficit during the early- to mid-vegetative stage (Carberry and Abrecht, 1991).
Delay silking by severe water or nitrogen stress simulate leaf area development by accounting for relationships between total leaf number and leaf area (Muchow and Carberry, 1989; Keating and Wafula, 1991) allow thermal time to accumulated between 0 and 10 oC, thus permitting the accurate simulation of phenological development in cool temperate environments (Wilson et al., 1995).
Determine transpiration based on biomass accumulation, a transpiration efficiency coefficient, daily vapour pressure deficit and a 0-1 soil water deficit factor. Uses a radiation-use efficiency based on above-ground biomass accumulation, and grows root biomass based on fixed root:shoot ratios for different phenological phases (Carberry et al. 1989) The model was validated on many of the same datasets that were originally used to develop CM-KEN and CM-SAT, in addition to new datasets (see Table below).
Maize Module Structure
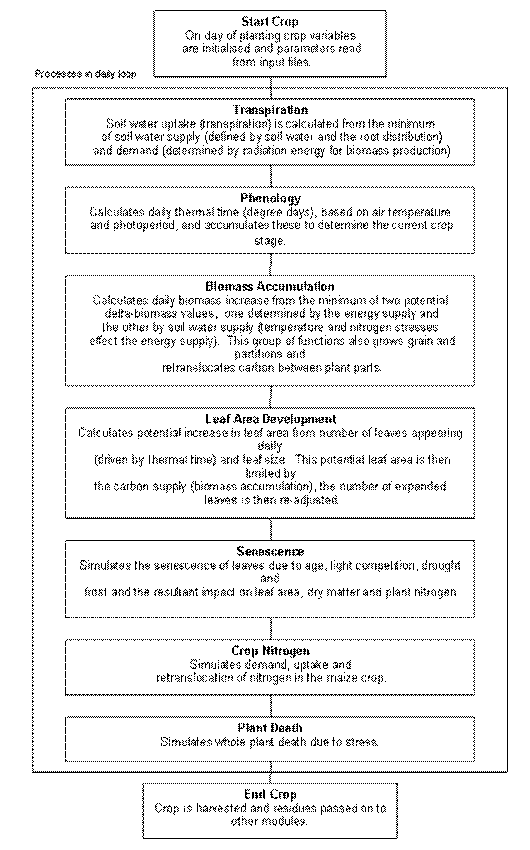
Phenology
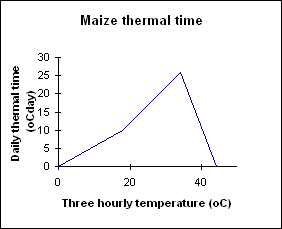
There are 11 crop stages and nine phases (time between stages) in the maize module, and commencement of each stage (except for sowing to germination which is driven by soil moisture) is determined by accumulation of thermal time. Each day the phenology routines calculate today’s thermal time (in degee days) from 3-hourly air tempertures interpolated from the daily maximum and minimum temperatures. Thermal time is calculated using the relationship in Figure 1 with the eight 3-hour estimates averaged to obtain the daily value of thermal time (in growing degree days) for the day. These daily thermal time values are cumulated into a thermal time sum which is used to determine the duration of each phase. Between the stage of emergence and flowering the calculated daily_thermal_time is reduced by water or nitrogen stresses, resulting in delayed phenology when the plant is under stress.
The thermal time between sowing and germination is dependent upon soil water levels. The phase between germination and emergence includes an effect of the depth of sowing on the thermal time target. The duration between emergence and flag leaf appearance is determined by the total number of leaves destined to appear on the plant, and the rate at which they appear, which is determined by temperature (see below). The total number of leaves is equal to the number in the seed at germination (7) plus the number subsequently initiated at a rate of 21 o Cdays per leaf, until floral initiation is reached. Hence the timing of floral initiation will determine the total leaf number and the timing of the appearance of the flag leaf and flowering (i.e. silking). The phase between emergence and floral initiation is composed of a cultivar-specific period of fixed thermal time, commonly called the basic vegetative or juvenile phase. Between the end of the juvenile phase and floral initiation the thermal development rate is sensitive to photoperiod (calculated as a function of day of year and latitude) if the cultivar is photoperiod sensitive. The model assumes that maize, as a short day plant, will have a longer phase (dependent upon cultivar) between the end of the juvenile phase and initiation if photoperiods exceed 12.5 hours. There are cultivar-specific fixed thermal time durations for the subsequent phases between flowering and the start of grain fill, between the start and end of grainfill, between the end of grainfill and maturity, and between maturity and harvest ripe.
Biomass accumulation (Photosynthesis)
Each day two estimates of the daily biomass production are calculated, one limited by available water for transpiraton (eqn 1), and the other limited by radiant energy (eqn 2). The minimum of these two estimates is the actual biomass production for the day.
1. delta_drymatter_transpiration = soil_ water_ supply * transpiration_efficiency
Note: transpiration_efficiency is derived from the transpiration_efficiency_coefficient (=0.009) and the vapour pressure deficit (vpd) estimated from daily temperatures.
2. dlt_drymatter_potential = rue *radiation_interception
Note rue (radiation-use efficiency) is 1.6 g MJ-1 from emergence to the start of grain-filling, and then declines to 1.06 g MJ-1 from the start of grain filling to account for the effects of leaf aging on reduced photosynthetic capacity (Muchow et al. 1990). Radiation interception is calculated from leaf area index and a radiation extinction coefficient of 0.45.
Biomass partitioning
Daily biomass production is partitioned to different plant parts in different ratios depending on crop stage. Until the end of juvenile phase the root:shoot ratio is maintained at 1.0, and then decreases to a value of 0.087 at flowering. Between emergence and flag leaf appearance the proportion of biomass produced that is partioned to leaf increases exponentially as leaves appear. Between the stage floral initiation and flag leaf appearance, the biomass remaining after allocation to leaf is allocated between stem and developing ear in the ration 1:0.30. After leaf growth has ceased at flag leaf appearance, biomass is partitioned between stem and ear only until the start of grain filling, whereuopon partitioning to grain only occurs. The maize module allows a total retranslocation of no more than 15 and 20% of leaf and stem biomass present at the start of grainfilling, respectively Grain demand for carbohydrate (biomass) is calculated by multiplying the grain number by the maximum potential grain growth rate (e.g. for Dekalb_XL82 10 mg/grain/day). The number of grains set per plant is determined by the average daily growth rate per plant between floral initiation and the start of grain filling, using the function developed by Edmeades and Daynard, (1979).
Leaf development
Leaf appearance rate is driven by thermal time, the last 14 leaves before the flag leaf appear each 36 o Cdays, before which a leaf appears every 65 o Cdays (Wilson et al., 1995).
Potential LAI
is a product of leaf number, leaf size, number of plants per m2 and the water stress factor for expansion (see water deficits section below). An adjustment factor is used to account for the area of currently expanding leaves. Leaf size is calculated from final leaf number assuming that it follows a bell-shaped distribution with leaf position along the stalk (Keating and Wafula, 1992). Early in crop development, before floral initiation is reached and hence before final leaf number is known, an estimated date of floral initiation is used to calculate a provisional final leaf number for the purposes of simulating leaf size.
Actual LAI
is less than the potential LAI if there is not sufficient biomass partitioned to leaf on that day. Maximum specific leaf area (SLA_MAX) defines the maximum leaf area (m 2 ) that can be expanded per gram of biomass. SLA_MAX declines with increasing LAI i.e. smaller, younger crops have larger thinner leaves.
Leaf senescence
There are four causes of leaf senesence; age, light competition, water stress and frost. The maize senescence routines calculate a senesced LAI for each stress each day and take the maximum of the four values as the day’s total senescence. A fraction of the oldest green leaf dies each day after flowering. This senescence due to age occurs a rate of leaves per day (this is calculated from the day’s thermal time divided by a constant leaf-death-rate). This number of dead leaves is then converted to a senesced LAI. Above an LAI of 4.0 light competition causes leaf area to be lost. The LAI senesced because of light competition is related to the amount LAI exceeds 4.0 (see eqns 3 and 4).
3. sensLAI_light_fac = 0.008 *(LAI- 4.0)
4. delta_sensLAI_light = LAI * sensLAI_light_fac eqn
Water stress during crop growth will cause leaf senescense (eqns 5 and 6).
5. sensLAI_water_fac = 0.05 * (1 – maize_swdef(photo))
6. delta_sensLAI_water = LAI * sensLAI_water_fac eqn
Note: the calculation of the water stress factor maize_swdef(photo) is descibed in the ‘water deficits’ section below. Frost senescence. Temperatures between 6.0 and 0 o C will cause a linearly increaseing loss of leaf area from 0 to 100% respectively. From the values of senesced LAI the maize module calculates the biomass and nitrogen in that leaf area that is senesced, however a proportion of the carbon and nitrogen of these leaves is retranslocated to stem before senescence.
Tillering
The potential tiller no. in the maize module has been set to 0, effectively disabling the tillering routine.
Regrowth
There are no regrowth routines in maize.
Water uptake
To determine the amount of water supply to the crop on any day, first the total available water above the lower limit for all soil layers with roots is summed (eqn 7). If roots are only partially through a layer available soil water is scaled to that portion that contains roots. The kl constant (value differs for each soil layer) is then used to limit the amount of water available on any day (eqn 8). The kl factor is emphirically derived, incorporating both plant and soil factors which limit rate of water uptake. do layer = 1, deepest_layer (do loop to calculate available water for all layers)
7. sw_avail = sw(layer) – ll (layer)
8. sw_supply(layer) = sw_avail * kl (layer)
Soil water demand is calculated as in the ‘biomass accumulation’ section above where potential biomass production is a function of radiation interception and rue . This potential biomass production is converted to water demand using transpiration efficiency. Transpiration efficiency is calculated from the transpiration effieicny coefficient ( transp_eff_cf ), which can vary with growth stage, and vapour pressure deficit. Soil water demand can be capped in the *.ini file by the atmospheric evaporative demand (eo) adjusted by the proportion of green canopy cover (cover_green) and a crop factor (eo_crop_factor) i.e. eo_crop_factor * eo * cover_green . Users wishing to use the eo_crop_factor should consult with the module owner. Water uptake is the minimum of the supply and demand.
Water deficits affecting plant growth
Soil water deficit factors are calculated to simulate the effects of water stress on different plant growth processes. Three water deficit factors are calculated which correspond to four plant processes each having different sensitivity to water stress i.e. photosynthesis (photo), phenology (pheno), and leaf-expansion (expansion). A water availability ratio is calculated by dividing actual soil water supply (sw – ll) by the potential soil water supply (dul – ll). This ratio is used in the relationships illustrated to derive the stress factors for photosynthesis and leaf expansion. A factor of 0 is complete stress and 1 no stress.
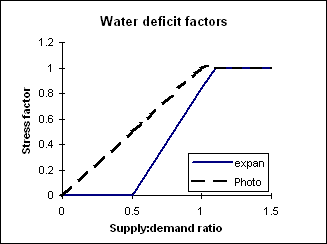
A fraction of plants (0.044) will be killed each day due to water stress once the cumulative water stress factor for photosynthesis exceeds 4.6. Nitrogen uptake and retranslocation In order to calculate nitrogen demand today, first potential biomass production is re-calculated unlimited by water, nitrogen or temperature i.e. as a function of rue and radiation-interception (eqn 2). This dry matter (biomass) is then partition into plant parts according to their current relative weights. The maize module has a defined minimum, critical and maximum N concentration for each plant part. Demand for nitrogen in each part attempts to maintain nitrogen at the critical (non stressed) level. Nitrogen demand on any day is the sum of the demands from the pre-existing biomass of each part required to reach critical N content, plus the N required to maintain critical N concentrations in today’s potentially assimilated biomass. A nitrogen uptake maximum is defined as the nitrogen uptake required to bring all plant part N contents to the maximum allowable concentration. Nitrogen supply is the sum of nitrogen available via mass flow (eqn 9) and by diffusion (eqn 10).
9. no3_massflow (layer) = no3_conc * delta_sw (layer)
10. no3_diffusion (layer) = sw_avail_frac *no3_conc
note: these layer values are summed to root depth and sw_avail_frac is ratio of extractable soil-water over total soil-water. If nitrogen demand cannot be satisfied by mass flow then it is supplied by diffusion. Demand can only be exceeded by supply from mass flow (up to the nitrogen uptake maximum). If both mass flow and diffusion supplies can’t satisfy demand then nitrogen is sought from N fixation (see next section). Nitrogen available for uptake is distributed to plant parts in proportion to their individual demands. Nitrogen for grain is retranslocated from other plant parts, N is not directly taken up from the soil or atmosphere to meet grain demand. Nitrogen is available for retranlocation from all parts except for grain and roots; other plant parts will translocate nitrogen until they reach their defined minimum N concentration. Grain nitrogen demand is again driven by critical N content but this demand is lowered if the plant is under N stress. Grain N demand is also affected by temperature and water stress using eqns 11 and 12 below.
11. N_grain_temp_fac = 0.69 + 0.125 * aver_temp
12 N_grain_sw_fac = 1.125 – 0.125 * swdef (expansion)
The greatest of these two factors is multiplied by the previously calculated N demand i.e. if temperature is high or sw deficit is low (water stressed) the N demand will be increased above the level required to reach the critical N concentration.
N fixation
There is no nitrogen fixation in the maize module.
Nitrogen deficits affecting plant growth
There are three N availability factors (0-1), one each for the photosynthesis, expansion, phenology and grain filling processes. A N concentration ratio is calculated for the stover (stem + leaf) in eqn 14 which is used as a measure of N stress, then different constants are used to convert that ratio to a deficit factor for each of the processes. A factor of 1 is used for effecting grain N concentration, 1.25 for photosynthesis (reduces rue), 0.8 for expansion (reduces leaf area expansion) and 5.75 to slow phenological development. As a value of 1 is no stress and 0 complete stress, phenology is least sensitive to nitrogen deficiency and grain N the most.
14. N_conc_ratio = (N_conc_stover – N_conc_stover_min) / (N_conc_stover_crit – N_conc_stover_min)
Root growth and distribution
Root depth is initialised at the depth of sowing. Between emergence and grain filling, the increase in root depth is a daily rate multiplied a soil water availability factor. The daily rate is 10-15 mm/day during emergence and 33mm/day from end-of-juvenile to the start of grain-filling. Root depth is constrained by the soil profile depth. The increase of root depth through a layer can be constrained by known soil constraints through the use of the 0-1 parameter xf, which is input for each soil layer. Growth of root biomass is partitioned with depth using an exponential decay function from the soil surface and converted to root length density using a fixed specific root length. Roots are not senesced during the life of the crop, but are incorporated in the soiln module at harvest and distributed as fresh organic matter in the profile
Temperature stress
There are no generic temperature factors, as for water and nitrogen stress, but as discussed in sections above temperature does influence grain N content, rate of senescence and radiation use efficiency (rue).
Plant death
All or some of the plants can be killed due to a variety of stresses; If the crop hasn’t germinated within 40 days of sowing, due to lack of germinating moisture, all plants are killed. If the crop does not emerge with 150 o Cdays of sowing, because it was sown too deep, then all plants are killed. If crop is past floral initiation and LAI = 0, then all plants are killed due to total senescence. If the cumulative phenological water stress factors exceed 25, all plants are killed due to water stress prolonging phenology. A fraction of plants will be killed by high temperatures immediately following emergence.
Detachment
The detachment routines in maize are disabled in the current code.
Maize Module Parameterisation
Crop lower limit and kl values are need for each soil layer
ll = 0.200 0.200 0.200 0.220 0.250 () ! crop lower limit
kl = 012 0.08 0.06 0.04 0.02 () ! kl need calibrating for each crop and soil type
Phenology and grainfilling parameters are needed for each cultivar. An example is given below of those for the katumani composite cultivar. Some of the parameters are not used in the current version, as they can be used in alternative options for simulating some processes (e.g. grain filling). (indicated below as option).
calibration.maize.katumani
| hi_incr | 0.018 (1/days) |
| hi_max_pot | 0.55 (g/g) |
| head_grain_no_max | 450 () |
| grain_gth_rate | 10.5 (mg/grain/day) |
| tt_emerg_to_endjuv | 150( o C day) |
| est_days_endjuv_to_init | 20 () |
| pp_endjuv_to_init | 10 |
| tt_endjuv_to_init | 0.0 ( o C day) |
| photoperiod_crit1 | 12.5 (hours) |
| photoperiod_crit2 | 24.0 (hours) |
| photoperiod_slope | 10.0 ( o C/hour) |
| tt_flower_to_maturity | 660 ! ( o C day) |
| tt_flag_to_flower | 10 ( o C day) |
| tt_flower_to_start_grain | 120 ( o C day) |
| tt_maturity_to_ripe | 1 ( o C day) |
Module Dependencies
The minimum module configuration required to run maize in APSIM is the inclusion of the report, input, manager, soilwat, soiln and residue and maize modules.
Crop Sowing and Harvesting Logic
Within the manager file the following syntax is used for harvest and planting the maize crop: if (maize.stage_name = ‘harvest_ripe’ and maize.plant_status = ‘alive’) then maize harvest maize kill_crop maize end_crop endif if (maize.plant_status = ‘dead’) then report do_output maize harvest maize end_crop endif if (day > 120 and day < 240 and maize.plant_status = ‘out’ ) then maize sow plants = 15 (p/m2), sowing_depth = 50 (mm), row_spacing = 0.35 (m), cultivar = katumani, fertile_tiller_no = 0 endif (note: row_spacing in sowing command is optional)
Skip Row Planting
maize sow plants = 15 (p/m2), sowing_depth = 50 (mm), row_spacing = 0.35 (m), cultivar = katumani, fertile_tiller_no = 0, skip = single
Skip row planting can be specified by using the skip keyword on the sowing command with a value of “single”, “double” or “solid”. A single skip has two crop rows followed by a single unplanted row whereas a double skip has two crop rows followed by two unplanted rows. A solid planting behaves as it no skip row information has been specified. Currently, the change to light interception is the only effect of the skip planting on the crop growth.
Maize Module Outputs
The following Maize variable can be output through the report module
| ===Variable Name=== | Units | Description | |
| stage | current phenological stage | ||
| stage_code | |||
| stage_name | |||
| crop_type | |||
| leaf_no | number of fully expanded leaves | ||
| leaf_no_dead | no of dead leaves | ||
| leaf_area (max_leaf = 1000) | mm 2 | leaf area of each leaf | |
| height | mm | canopy height | |
| root_depth | mm | depth of roots | |
| rlv | mm.mm -3 | root length per volume of soil in each soil layer | |
| hi | Harvest index | ||
| plants | plants/m 2 | plant density | |
| grain_no | grains/plant | grain number | |
| grain_size | g | individual grain wt | |
| cover_green | 0-1 | fraction of radiation reaching the canopy that is intercepted by green leaves | |
| cover_tot | 0-1 | total crop cover fraction | |
| lai_sum | leaf area index of all leaf material live + dead | ||
| tlai | tot lai | ||
| slai | area of leaf that senesces from plant | ||
| lai | m 2 /m 2 | live plant green lai | |
| tlai_dead | m 2 /m 2 | total lai of dead plants | |
| root_wt | g/m 2 | root biomass | |
| leaf_wt | g/m 2 | leaf biomass | |
| stem_wt | g/m 2 | stem biomass | |
| grain_wt | g/m 2 | grain biomass | |
| grain_wt | g/m 2 | grain biomass | |
| dm_green (max_part = 6) | g/m 2 | live plant dry weight (biomass) | |
| dm_senesced (max_part = 6) | g/m 2 | senesced plant dry wt | |
| dm_dead (max_part = 6) | g/m 2 | dry wt of dead plants | |
| yield | kg/ha | grain yield dry wt | |
| biomass | kg/ha | total above-ground biomass | |
| stover | kg/ha | above-ground biomass not including grain | |
| dlt_dm | g/m 2 | the daily biomass production | |
| dlt_dm_green (max_part = 6) | g/m 2 | plant biomass growth | |
| n_green (max_part = 6) | g/m 2 | plant nitrogen content | |
| n_senesced (max_part = 6) | g/m 2 | plant n content of senesced plant | |
| n_dead (max_part = 6) | g/m 2 | plant n content of dead plants | |
| dlt_n_green (max_part = 6) | g/m 2 | actual n uptake into plant | |
| dlt_n_retrans (max_part = 6) | g/m 2 | nitrogen retranslocated out from parts to grain | |
| dlt_n_detached (max_part = 6) | g/m 2 | actual n loss with detached plant | |
| dlt_n_dead_detached (max_part = 6) | g/m 2 | actual n loss with detached dead plant | |
| swdef_pheno | 0-1 | water deficit factor for phenology | |
| swdef_photo | 0-1 | water deficit factor fo photosynthesis | |
| swdef_expan | 0-1 | water deficit factor for leaf expansion | |
| ep (num_layers) | mm | water uptake in each layer | |
| cep | mm | cumulative water uptake | |
| sw_demand | mm | total crop demand for water | |
| sw_supply | mm | total supply over profile | |
| esw_layer (num_layers) | mm | plant extractable soil water | |
| n_conc_stover | % | sum of tops actual n concentration | |
| n_conc_crit | % | sum of tops critical n concentration | |
| n_grain_pcnt | % | grain n concentration percent | |
| n_uptake_grain | g/m 2 | n uptake by grain | |
| n_uptake | g/m 2 | cumulative total n uptake by plant | |
| n_uptake_stover | g/m 2 | n uptake by stover | |
| no3_tot | g/m 2 | total no3 in the root profile | |
| n_demand | g/m 2 | sum n demand for plant parts | |
| n_supply | g/m 2 | n supply for grain | |
| n_supply_soil | g/m 2 | n supply from soil | |
| n_fix_pot | g/m 2 | potential N fixation | |
| nfact_photo | N deficit factor for photosynthesis | ||
| nfact_grain | N deficit factor for grain N content | ||
| nfact_photo | 0-1 | Nitrogen stress factor for photosynthesis | |
| nfact_expan | 0-1 | Nitrogen stress factor for cell expansion | |
| dlt_tt | o Cday | daily thermal time | |
| das | days after sowing | ||
Maize Module validation
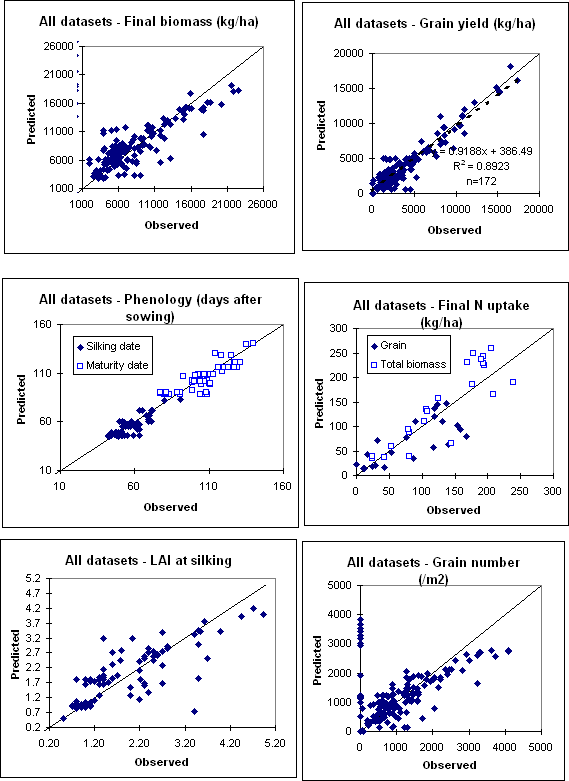
The maize model was validated against a wide range of datasets originating from tropical and sub-tropical Australia , semi-arid Kenya and USA (Table 1). Overall model performance with a combined set of this data is presented in the following figure. Overall, model performance was good, particularly for grain yield, usually the most important variable to be simulated. The range in grain yield covered 0 to 17.3 t ha -1 . The r-squared value for observed versus predicted grain yield was 89%.
Table 1: Details of datasets used to validate the maize crop module.
| Factors
|
Location
|
Reference
|
| Sowing date, water supply, N fertiliser rate, plant population density
|
Tropical Australia
|
Muchow (1989a,b), Carberry et al., (1989), Sinclair and Muchow (1995)
|
| Sowing date, N fertiliser rate
|
Sub-tropical Australia
|
Wilson , et al. (1995), Muchow (1994)
|
| Sowing date, N fertiliser rate, variety, water supply, plant population density
|
Semi-arid Kenya
|
Keating et al. (1992)
|
| Sowing date, plant population density
|
USA
|
Muchow et al. (1990)
|
Inspection of model performance for individual experiments shows that it is simulating the key responses to major agronomic variables. For example the following figures show the model performance for responss to plant population density under both deficit and favourable water (bmw6 experiment conducted at Katumani, Kenya with both the dryland composite DLC and Katumani composite KCB cultivars) and nitrogen (jmw2 experiment conducted at Kiboko, Kenya with the KCB cultivar) supply.
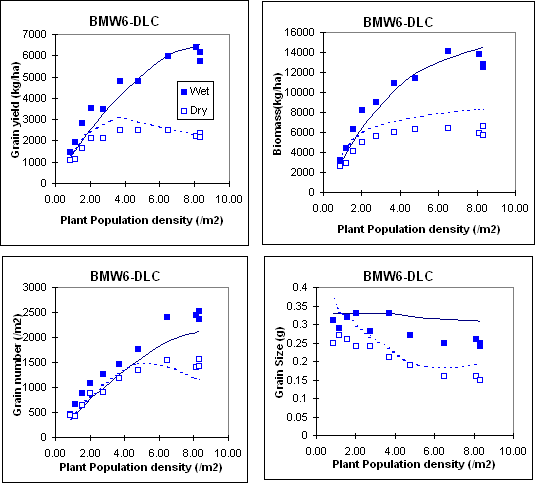
References
Carberry, P. S.; Muchow, R. C. and McCown, R. L. 1989. Testing the CERES-Maize simulation model in a semi-arid tropical environment. Field Crops Research, 20: 297-315.
Carberry, P. S. and Abrecht, D. G., 1991. Tailoring crop models to the semi-arid tropics: In: RC Muchow and JA Bellamy (Eds) Climatic risk in crop production: Models and management in the semi-arid tropics and sub-tropics. Cab International, Wallingford . P. 157-182.
Edmeades, G. O. and Daynard, T. B. 1979. The relationship between final yield and photosynthesis at flowering in individual maize plants. Canadian Journal of Plant Science 59: 585-601.
Jones, C. A.and Kiniry, J. R. 1986. CERES-Maize: A simulation model of maize growth and development. Texas A & M University Press, College Station , texas, 194pp.
Keating, B. A.; Godwin, D. C.; Watiki, J. M. 1991. Optimising nitrogen inputs in response to climatic risk. In: RC Muchow and JA Bellamy (Eds) Climatic risk in crop production: Models and management in the semi-arid tropics and sub-tropics. Cab International, Wallingford . P. 329-358.
Keating, B. A. and Wafula, B. M. 1992. Modelling the fully-expanded area of maize leaves. Field crops Research, 29: 163-176.
Keating, B. A., Wafula, B. M. and watiki, J. M. 1992. Development of a modelling capability for maize in semi-arid eastern Kenya . In: Probert, M. E. (1992) A search for strategies for sustainable dryland cropping in semi-arid eastern kenya . Proceedings of a Symposium held in Nairobi , kenya , 10-11 December 1990. ACIAR Proceedings No. 41, 138 pp.
Muchow, R. C. 1989. Comparative productivity of maize, sorghum and pearl millet in a semi-arid tropical environment. I. Yield potential. Field Crops Research 20: 191-205.
Muchow, R. C. 1989. Comparative productivity of maize, sorghum and pearl millet in a semi-arid tropical environment. II. Effect of water deficits. Field Crops Research 20: 207-219.
Muchow, R. C. 1994. Effect of nitrogen on yield determination in irrigated maize in tropical and subtropical environments. Field Crops Research 38: 1-13.
Muchow, R. C. and Carberry, P. S. 1990. Phenology and leaf area development in a tropically-adapted maize. Field Crops Research, 20: 221-236.
Muchow, R. C., Sinclair, T. R. and Bennett, J. M. 1990. Temperature and solar radiation effects on potential maize yield across locations. Agronomy Journal 82: 338-343.
Sinclair, T. R. and Muchow, R. C. 1995. Effect of nitrogen supply on maize yield: I. Modeling physiological responses. Agronomy Journal 87: 632-641.
Wilson, D. R.; Muchow, R. C. and Murgatroyd, C. J. 1995. Model analysis of temperature and solar radiation limitations to maize potential productivity in a cool climate. Field Crops Research, 43: 1-18.
